20 行 Python 代码说清量子霸权!
- 2019-10-29 17:47:31
- 来源:搜狐科技
- 0
- 0
- 添加收藏

作者 | 马超
出品 | 程序人生(ID:coder_life)
近日谷歌的有关量子霸权的论文登上了Nature杂志150年刊的封面位置,而再次罢占各大媒体的头条位置,其实这篇文章(https://www.nature.com/articles/s41586-019-1666-5)之前曾经短暂上过NASA的网站,笔者也曾经介绍过过相关论文的情况详见https://blog.csdn.net/BEYONDMA/article/details/101151544?utm_source=app,而这次美国的伊万卡公主甚至也直接发推,官宣美国实现量子霸权。
虽然这次谷歌的论文中声称他们的量子计算机仅用200秒就完成了传统计算机需要上万年才完成的任务,不过ibm等公司也公开回怼称,如果优化算法超算也仅需要几天时间就可以完成,完全谈不上什么霸权。其实笔者后面也会讲道量子计算应用的领域有限,此次的量子采样任务也的确和量子霸权关系不大,媒体略显过度炒作了,笔者本文继续使用最通俗的语言与代码来带各位读者体验一下量子霸权。
什么是量子霸权
通俗的讲就是量子计算机碾压传统超算的算力。量子计算的速度之源其实是量子比特,以谷歌本次所讲的量子芯片为例,其内部构造如下:
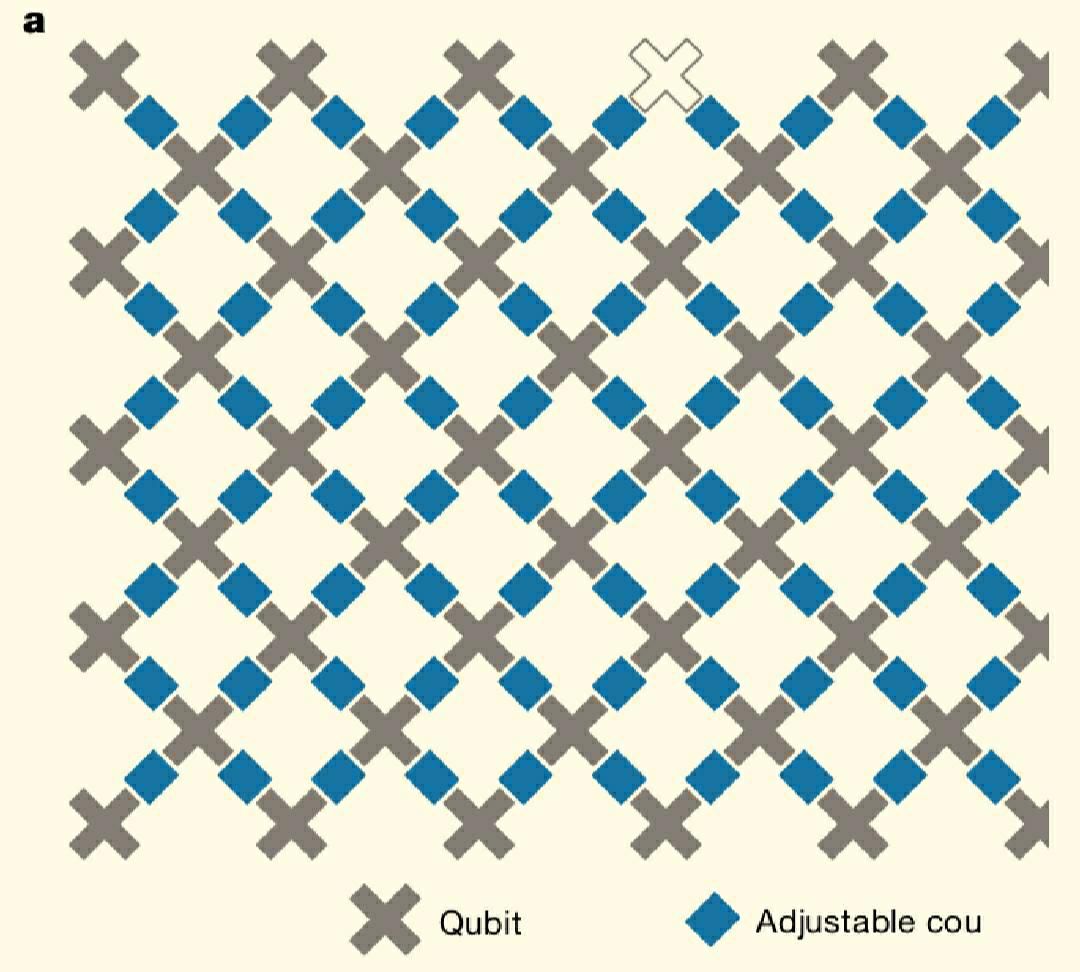
我们可以看到与传统芯片不同的是量子单元由于量子纠缠的存在是有特定的关联关系的,这种不同计算单元中存在的纠缠关系是传统超算各计算单元所不具备的性质。以IBM有关leverage secondary Storage.的论文所述例子如下,当然这只是文中片断仅用于示例:
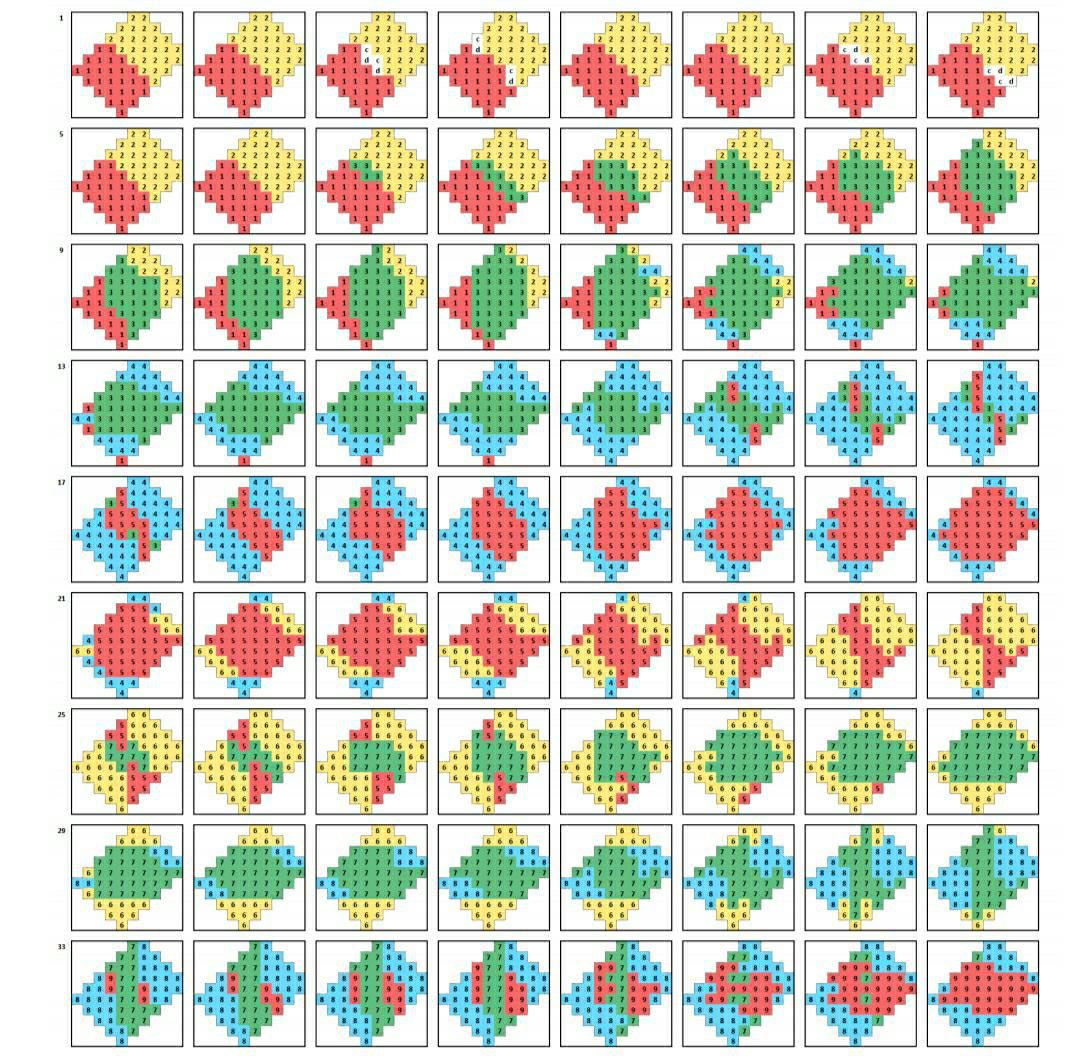
也就是说在某种特定任务的情况下,量子芯片每增加一个量子单元那么它的算力可以呈指数级上涨,而传统计算机每增加一个CPU其算力只能线性上涨。那么随着量子单元的增加,量子芯片的计算能力必将远超现在的超算。
量子计算的限制
由于量子单元所表示的量子经特并不是简单的0和1,还有叠加态与相互的纠缠态,其数学表达式非常复杂,无法用于通用计算,对于每种计算任务都需要为量子计算单独设计算法。换言之量子计算机并不是通用计算机,只能用于特定的任务。
量子霸权的由来
由于量子计算的性质十分复杂,需要非常高超的数学知识才难设计量子算法,而且应用的领域不广,所以在很长一段时间里人们还没有太重视量子计算机的发展,直到用于因式分解的量子算法shor横空出世,说起来其基本并不复杂,具体如下:
步骤1.随机取正整数a,a
步骤2.定义函数,求函数f(x)的周期r,如果r为奇数则重取a,再求r,直到r为偶数为止。
步骤3.由和可用的辗转相除法求与N的最大公约数n1,n1即为N的一个因子。至此N的因式分解即完成。
这个算法的精髓就是步骤2,它将因式分解问题转化为了求周期r的问题,而求周期的小能手傅里叶变换恰是量子计算的擅长所在。我们知道傅里叶变换是将函数由时域映射到频率域的过程,而频率就是周期的倒数,所以周期问题可以以用傅里叶变换求解,而傅里叶变换的算子与量子比特契合度较高,是量子计算的拿手好戏。所以所谓量子霸权的逻辑是SHOR算法能够攻破rsa算法,而rsa算法又是整个信息安全的基石,所以掌握了量子计算机就等于破解了整个信息安全身份认证体系,从而实现霸权。可以说如果没有SHOR算法的提出,那么也就没有量子霸权的概念了。
用Python体验量子算法
目前IBM推出的qiskit是非常棒的Python量子模拟器,不过最近新注册用户可能有些困难。如果各位读者之前有IBM Q的帐号可以到他们在线的Notebookhttps://quantum-computing.ibm.com/jupyter环境去感受一直量子傅里叶变换,当然读者如果有Python3.6和C++的编程环境,直接使用pip install qiskit命令即可完成安装, 具体量子傅氏变换的代码及注释整理如下:
import math
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
import warnings #忽略告警
warnings.filterwarnings( 'ignore')
#定义量子傅里叶变换函数qft
def qft(circ, q, n):
"""n-qubit QFT on q in circ."""
forj in range(n):
fork in range(j):
circ.cu1(math.pi/float( 2**(j-k)), q[j], q[k]) #套用傅里叶就换
circ.h( q[j])
n = 3#量子比特数量
q= QuantumRegister(n)
c = ClassicalRegister(n)
qft_n = QuantumCircuit( q, c) #定义量子电路,后面可以可视化
qft(qft_n, q, n)
fori in range(n):
qft_n.measure( q[i], c[i])
print(qft_n.qasm)
# 可视化
from qiskit.tools.visualization import circuit_drawer
circuit_drawer(qft_n,filename= './qft_circuit') #可视化
然后打开在你运行以上代码的目录打开qft_circuit文件就能看到咱们刚刚定义的量子电路了,具体效果如下:
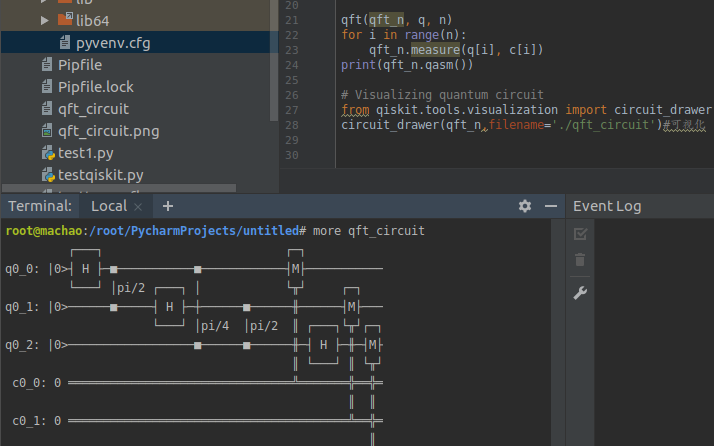
谷歌所做的工作
本次谷歌的量子计算机是一块包含54个量子比特的超导量子计算芯片Sycamore ,不过可惜的是其中一个比特损坏了,所以实际是53量子比特,它使用超低温状态下的铝实现约瑟夫森结,整体运行在20mK以下的环境,以保证超导的状态。
本次的计算任务是量子采样,简单的理解就是量子状态的采集,这个任务可以被广泛应用在量子力学的研究中。根据结果来看Sycamore 200秒约可采样100万次,并且最终结果的保真度预计有0.2%;作为对比,谷歌预计超算 Summit 要得到保真度为0.1% 的结果,需要耗费1万年。
不过值得一提的由于SHOR算法要求的计算错误率不能超过0.7%,所以目前以Sycamore 的精度还不能承担破解rsa体系的任务。由于量子不确定性效应,随着量子比特的增加,控制整个计算芯片的难度也大大增加,谷歌科学们甚至提出了使用机器学习的方式,这在我之前的博客中已经有说明了(https://blog.csdn.net/BEYONDMA/article/details/101151544?utm_source=app)这里不加赘述了,不过能实现如此多单元的量子计算机也实属创举。
写在最后
虽然量子计算只能应用于特定场景,且量子霸权主要也主要是指量子计算可以破解rsa安全体系,但是也不能否定本次谷歌在量子计算领域的进展与成果。客观的讲谷歌只是迈向了通向量子霸权之路的第一步,但是所有伟大的IT项目都是从“hello world”做起的。
用谷歌CEO皮柴的话讲这就是这一里程碑对量子计算世界的意义:一个充满可能性的时刻。
☞20 行 Python 代码说清量子霸权!