42，人类破解宇宙生命终极答案，竟是3个整数立方和

　　[新智元导读]42，可以写成3个整数的立方和！这是数学界的一大突破，由MIT和布里斯托大学的数学家共同发现，他们以“生命、宇宙以及一切”的网页标题，公布了这一成果。

　　人类第一次将42写成了3个整数的立方和！

　　昨天，有人在 MIT 数学系的网站上贴出一个等式，网页很简单，但没给出结果：

　　（-80538738812075974）^3 + 80435758145817515^3 + 12602123297335631^3

　　等于 42！

　　在推特上，菲尔兹奖得主高尔斯也转发了这个结果。

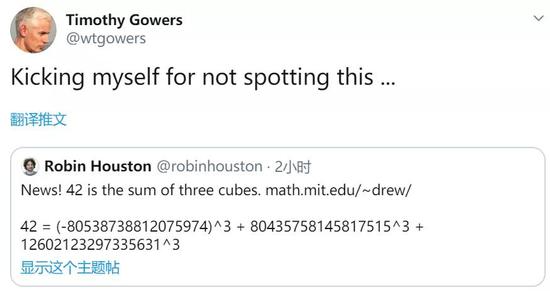
　　这是一个大新闻，因为至此，下面这句话成为了定理：

　　除了 9n±4 型自然数外，所有 100 以内的自然数都能写成三个整数的立方和。

　　是的，在此之前，42是100以内最后一个尚未找到立方和的整数解的自然数。现在，这个解也找到了。

　　找到这个等式的数学家是来自布里斯托大学的 Andrew Booker 和来自麻省理工学院的Andrew Sutherland。

　　Andrew Booker 是布里斯托大学数学教授

　　今年3月， Andrew Booker 找到了33的立方和整数解，同样引起数学界轰动。昨天，Andrew Booker穿着印有“42”的T恤接受采访，解释了他们的研究过程。

　　在被问到“你们解决这个问题后，有没有兴奋得跳起来”时，Booker说：“我这次倒是没有跳起来，但是你知道，解决一个三、四十年来一直悬而未决的问题，实在是令人很满足！当然，这个论题本身还没有解决，下一个数字是114……”

　　有意思的是，两位数学家公布这一结果的网页标题是“生命、宇宙以及一切”（Life， the Universe and Everything）。

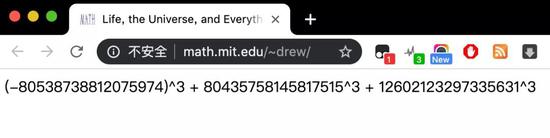
　　在道格拉斯·亚当斯著名的《银河系漫游指南》系列中，42是“生命、宇宙以及一切的终极答案”。

　　茫茫宇宙中，一个 “具有超级智慧的泛维度种族” 对关于生命意义的无休止的争论感到厌烦了，他们决定一劳永逸地解决这个问题。他们建造了宇宙一切空间和时间中第二强大的电脑 “沉思”，向它寻求 “关于生命、宇宙，以及一切的终极答案”。

　　整整 750 万年后，“沉思” 给出了答案 —42。

　　面对这个玄妙的答案，泛维度种族需要回过头先弄明白生命宇宙以及一切的终极问题，方能理解答案。但 “沉思” 不能胜任此项艰巨的任务，它说：“你们需要一台能够计算出这个终极答案的电脑，这台电脑具有无限和微妙的复杂性，以至于有机生命本身将会成为操作母体的一部分。你们自身也会以一种新的生命形式投入到这台电脑中，去操控为期 1000 万年的程序。我将会为你们设计出这台电脑，并且我已为它取好名字。它将会被称为…… 地球。”

　　痴迷、痴狂！人类寻找三立方数和简史

　　人类为什么对这样一个等式如此着迷呢？

　　这个问题至少可以追溯到 1825 年，数学家想知道，如果给定整数 K，是否存在整数 X、Y、Z，满足：

　　X^3 + Y^3 + Z^3 = K。

　　数论领域下有一大分支叫“丢番图方程”：

　　x^3+y^3+z^3=k 是否存在整数解是丢番图方程中的一个问题。

　　丢番图 （Diophantine） 是一位古希腊的大数学家，被认为是第一位懂得使用符号代表数来研究问题的人。

　　丢番图和他的墓志铭

　　其中丢番图最著名的事迹可能就是他的墓志铭 —— 曾经连续多年出现在各地中小学生的寒假作业扩展训练上：

　　坟中安葬着丢番图。

　　多么令人惊讶，它忠实地记录了所经历的道路。

　　上帝给予的童年占六分之一，

　　又过十二分之一，两颊长胡，

　　再过七分之一，点燃起结婚的蜡烛。

　　五年之后天赐贵子，

　　可怜迟到的宁馨儿，享年仅及其父之半，便进入冰冷的墓。

　　悲伤只有用数论的研究去弥补，

　　又过四年，他也走完了人生的旅途。

　　回到丢番图方程，由于立方数模 9 同余 0、1 或 - 1，三立方数和模 9 不可能同余 4 或 5，因而这是整数解存在的一个必要条件。因此9k+4或9k+5这种形式的整数不能写成三个立方数之和。然而，对于该条件是否同时为充分条件目前仍未有定论。

　　1992年，牛津大学的Roger Heath-Brown提出猜想，即其它所有整数都可以用无穷多种不同的方式写成三个立方体的和。在那以后，数学家们似乎已经被Heath-Brown的论点所说服，然而，找到把任何特定的数写成三个立方体之和的方法仍然是一个难题。

　　2000年，哈佛大学的Noam Elkies提出了一个实用的算法来寻找这类解。Elkies和其他数学家使用类似的方法，成功地为许多较小的整数找到了立方和的整数解。

　　2015年，数学家Tim Browning录制了一段视频，解释了这个问题。在那个时候，只有33、42和74这三个小于100的整数尚未找到解。这段视频让更多的人注意到了这个问题，并带来了一系列的突破。

　　Tim Browning的视频让更多数学家关注这个问题

　　受到这段视频的启发，几个月后，Sander Huisman找到了74的立方和整数解：

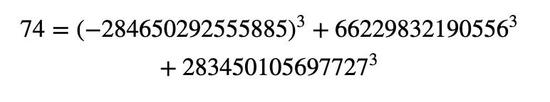
　　Tim Browning再次录制了一段关于Huisman解决74的视频。另一位数学家，即布里斯托大学的Andrew Booker看到了这段视频，决定解决这个问题。

　　他提出了一种新的算法，这种算法能更有效地找到一个特定数字的解。2019年2月27日，Booker公布了33的立方和整数解。

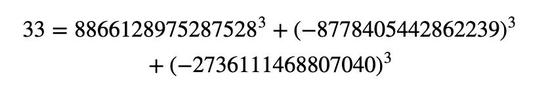
　　昨天，42也被解决了！Andrew Sutherland和Andrew Booker同时更新他们的主页，报告了42的立方和的整数解：

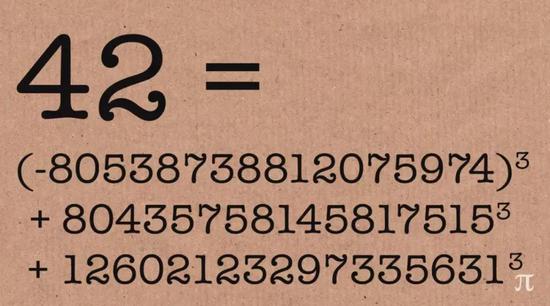
　　这意味着100以内的自然数的立方和的整数解全部找到！

　　1000以内还没找到解的整数只剩下：114，165，390，579，627，633，732，906，921 和 975。

　　100 以内三立方和的非零解全表

　　最后，附上 100 以内三立方和的非零解全表（多种写法选取其中一个）：

　　1 = （-1）³ + 1³ + 1³

　　2 = 7³ + （-5）³ + （-6）³

　　3 = 1³ + 1³ + 1³

　　4 不可能

　　5 不可能

　　6 = （-1）³ + （-1）³ + 2³

　　7 = 104³ + 32³ + （-105）³

　　8 = （-1）³ + 1³ + 2³

　　9 = 217³ + （-52）³ + （-216）³

　　10 = 1³ + 1³ + 2³

　　11 = （-2）³ + （-2）³ + 3³

　　12 = 7³ + 10³ + （-11）³

　　13 不可能

　　14 不可能

　　15 = （-1）³ + 2³ + 2³

　　16 = （-511）³ + （-1609）³ + 1626³

　　17 = 1³ + 2³ + 2³

　　18 = （-1）³ + （-2）³ + 3³

　　19 = 19³ + （-14）³ + （-16）³

　　20 = 1³ + （-2）³ + 3³

　　21 = （-11）³ + （-14）³ + 16³

　　22 不可能

　　23 不可能

　　24 = （-2901096694）³ + （-15550555555）³ + 15584139827³

　　25 = （-1）³ + （-1）³ + 3³

　　26 = 297³ + 161³ + （-312）³

　　27 = （-1）³ + 1³ + 3³

　　28 = 14³ + 13³ + （-17）³

　　29 = 1³ + 1³ + 3³

　　30 = （-283059965）³ + （-2218888517）³ + 2220422932³

　　31 不可能

　　32 不可能

　　33 = 8866128975287528³ + （-8778405442862239）³ + （-2736111468807040）³

　　34 = （-1）³ + 2³ + 3³

　　35 = 14³ + （-8）³ + （-13）³

　　36 = 1³ + 2³ + 3³

　　37 = 50³ + 37³ + （-56）³

　　38 = 1³ + （-3）³ + 4³

　　39 = 117367³ + 134476³ + （-159380）³

　　40 不可能

　　41 不可能

　　42 = （-80538738812075974）³ + 80435758145817515³ + 12602123297335631³

　　43 = 2³ + 2³ + 3³

　　44 = （-5）³ + （-7）³ + 8³

　　45 = 2³ + （-3）³ + 4³

　　46 = （-2）³ + 3³ + 3³

　　47 = 6³ + 7³ + （-8）³

　　48 = （-23）³ + （-26）³ + 31³

　　49 不可能

　　50 不可能

　　51 = 602³ + 659³ + （-796）³

　　52 = 23961292454³ + 60702901317³ + （-61922712865）³

　　53 = （-1）³ + 3³ + 3³

　　54 = （-7）³ + （-11）³ + 12³

　　55 = 1³ + 3³ + 3³

　　56 = （-11）³ + （-21）³ + 22³

　　57 = 1³ + （-2）³ + 4³

　　58 不可能

　　59 不可能

　　60 = （-1）³ + （-4）³ + 5³

　　61 = 845³ + 668³ + （-966）³

　　62 = 3³ + 3³ + 2³

　　63 = 7³ + （-4）³ + （-6）³

　　64 = （-1）³ + 1³ + 4³

　　65 = 91³ + 85³ + （-111）³

　　66 = 1³ + 1³ + 4³

　　67 不可能

　　68 不可能

　　69 = 2³ + （-4）³ + 5³

　　70 = 11³ + 20³ + （-21）³

　　71 = （-1）³ + 2³ + 4³

　　72 = 7³ + 9³ + （-10）³

　　73 = 1³ + 2³ + 4³

　　74 = （-284650292555885）³ + （66229832190556）³ + （283450105697727）³

　　75 = 4381159³ + 435203083³ + （-435203231）³

　　76 不可能

　　77 不可能

　　78 = 26³ + 53³ + （-55）³

　　79 = （-19）³ + （-33）³ + 35³

　　80 = 69241³ + 103532³ + （-112969）³

　　81 = 10³ + 17³ + （-18）³

　　82 = （-11）³ + （-11）³ + 14³

　　83 = （-2）³ + 3³ + 4³

　　84 = （-8241191）³ + （-41531726）³ + 41639611³

　　85 不可能

　　86 不可能

　　87 = （-1972）³ + （-4126）³ + 4271³

　　88 = 3³ + （-4）³ + 5³

　　89 = 6³ + 6³ + （-7）³

　　90 = （-1）³ + 3³ + 4³

　　91 = 364³ + 192³ + （-381）³

　　92 = 1³ + 3³ + 4³

　　93 = （-5）³ + （-5）³ + 7³

　　94 不可能

　　95 不可能

　　96 = 10853³ + 13139³ + （-15250）³

　　97 = （-1）³ + （-3）³ + 5³

　　98 = 14³ + 9³ + （-15）³

　　99 = 2³ + 3³ + 4³

　　100 = 7³ + （-3）³ + （-6）³